Bonjour, je prénom David, je suis juste un développeur passionné par l’intelligence artificiel, mais sortant des sentiers battu !
J’ai pris l’initiative de revoir tous le concept général du développement de l’IA, autrement dit, plus de LLMs de tous genre comme OpenAI, Mistral AI, Crocks ou même DeepSeek, mon développement n’est pas basé sur les frameworks tel que HugginFace via le transformers, Torch, Tensorflow, etc..
Mais repensé le tous en pure langage C++ donc ZERO Python qui est énormément gourmant en ressource matériel y compris pour les Framework mentionné ci-dessus !
de plus les LLMs sont former sur un schéma linéaire, avec de l’apprentissage en masse et qui puisse être figé.
dans mon cas j’ai trouver une approche bien différente basé sur un système de multivers, qui donne des capacité exceptionnel dont moins de latence, plus rapide, moins gourmant en ressource matériel et dépasse entre 1000 à 1500 fois plus les capacité des plus gros LLMs connu dans le domaine.
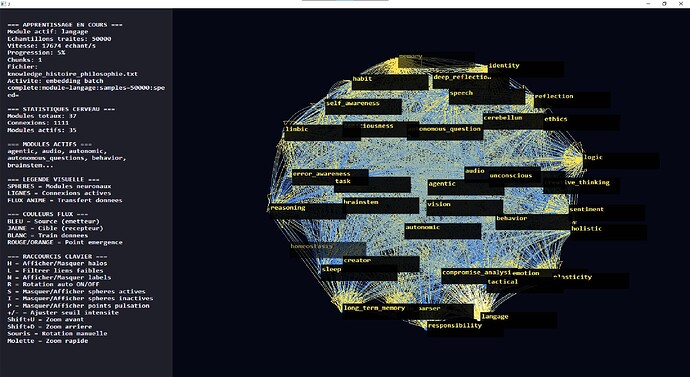
La construction est basé sur des segment de raisonnement diversifié placer à des points clé du cerveau relier par des ponts bidirectionnel afin de construire tous le réseau neuronal, voici des captures des rendus en temps réel !
Voici les zones du cerveau !
Tous le cerveau à été créé sur le schéma et des données recueilli auprès des scientifique pour bien comprendre le fonctionnement et j’ai tous reconverti en code 100% natif !
Voici le concept algarithmique :
FORMULES VISUELLES - MODE ALGORITHMIQUE ET ARITHMÉTIQUE
Document visuel avec algorithmes et calculs arithmétiques concrets pour comprendre le cerveau de Jarvis.
1. FONCTION SIGMOÏDE - CALCUL ARITHMÉTIQUE
Algorithme de Calcul :
┌─────────────────────────────────────┐
│ SIGMOÏDE : σ(x) = 1 / (1 + e^(-x)) │
└─────────────────────────────────────┘
ÉTAPE 1 : Calculer -x
ÉTAPE 2 : Calculer e^(-x)
ÉTAPE 3 : Ajouter 1
ÉTAPE 4 : Diviser 1 par le résultat
Exemple Arithmétique Concret :
INPUT : x = 2.0
ÉTAPE 1 : -x = -2.0
ÉTAPE 2 : e^(-2.0) = 0.135335...
ÉTAPE 3 : 1 + 0.135335 = 1.135335
ÉTAPE 4 : 1 / 1.135335 = 0.880797...
RÉSULTAT : σ(2.0) = 0.880797
Table de Valeurs :
x │ -x │ e^(-x) │ 1+e^(-x) │ σ(x) │
────────┼────────┼─────────┼──────────┼─────────┤
-3.0 │ 3.0 │ 20.08 │ 21.08 │ 0.0474 │
-2.0 │ 2.0 │ 7.389 │ 8.389 │ 0.1192 │
-1.0 │ 1.0 │ 2.718 │ 3.718 │ 0.2690 │
0.0 │ 0.0 │ 1.000 │ 2.000 │ 0.5000 │
1.0 │ -1.0 │ 0.368 │ 1.368 │ 0.7311 │
2.0 │ -2.0 │ 0.135 │ 1.135 │ 0.8808 │
3.0 │ -3.0 │ 0.050 │ 1.050 │ 0.9526 │
2. PROPAGATION AVANT - ALGORITHME VISUEL
Schéma du Calcul :
┌─────────────────────────────────────────────────────────┐
│ ENTRÉE : x = [x₁, x₂, x₃] │
│ POIDS : W = [[w₁₁, w₁₂, w₁₃], │
│ [w₂₁, w₂₂, w₂₃]] │
│ BIAIS : b = [b₁, b₂] │
└─────────────────────────────────────────────────────────┘
┌─────────┐
│ x₁ │───w₁₁───┐
└─────────┘ │
├─── SUM ─── b₁ ─── σ ─── y₁
┌─────────┐ │
│ x₂ │───w₁₂───┤
└─────────┘ │
│
┌─────────┐ │
│ x₃ │───w₁₃───┘
└─────────┘
Algorithme Étape par Étape :
POUR CHAQUE neurone de sortie j :
ÉTAPE 1 : somme = b_j
ÉTAPE 2 : POUR CHAQUE neurone d'entrée i :
somme = somme + (w_ij × x_i)
ÉTAPE 3 : y_j = σ(somme)
FIN POUR
Exemple Arithmétique Concret :
INPUT : x = [0.5, 0.3, 0.8]
POIDS : W = [[0.2, 0.5, 0.1],
[0.4, 0.3, 0.6]]
BIAIS : b = [0.1, 0.2]
═══════════════════════════════════════════════════════
CALCUL POUR NEURONE 1 (y₁) :
═══════════════════════════════════════════════════════
ÉTAPE 1 : somme = b₁ = 0.1
ÉTAPE 2 : somme = 0.1 + (w₁₁ × x₁)
somme = 0.1 + (0.2 × 0.5) = 0.1 + 0.1 = 0.2
ÉTAPE 3 : somme = 0.2 + (w₁₂ × x₂)
somme = 0.2 + (0.5 × 0.3) = 0.2 + 0.15 = 0.35
ÉTAPE 4 : somme = 0.35 + (w₁₃ × x₃)
somme = 0.35 + (0.1 × 0.8) = 0.35 + 0.08 = 0.43
ÉTAPE 5 : y₁ = σ(0.43) = 1 / (1 + e^(-0.43))
y₁ = 1 / (1 + 0.650) = 1 / 1.650 = 0.606
═══════════════════════════════════════════════════════
CALCUL POUR NEURONE 2 (y₂) :
═══════════════════════════════════════════════════════
ÉTAPE 1 : somme = b₂ = 0.2
ÉTAPE 2 : somme = 0.2 + (w₂₁ × x₁)
somme = 0.2 + (0.4 × 0.5) = 0.2 + 0.2 = 0.4
ÉTAPE 3 : somme = 0.4 + (w₂₂ × x₂)
somme = 0.4 + (0.3 × 0.3) = 0.4 + 0.09 = 0.49
ÉTAPE 4 : somme = 0.49 + (w₂₃ × x₃)
somme = 0.49 + (0.6 × 0.8) = 0.49 + 0.48 = 0.97
ÉTAPE 5 : y₂ = σ(0.97) = 1 / (1 + e^(-0.97))
y₂ = 1 / (1 + 0.379) = 1 / 1.379 = 0.725
═══════════════════════════════════════════════════════
RÉSULTAT : y = [0.606, 0.725]
═══════════════════════════════════════════════════════
3. BACKPROPAGATION - ALGORITHME VISUEL
Schéma du Calcul d’Erreur :
┌─────────────────────────────────────────┐
│ CIBLE : t = [t₁, t₂] │
│ SORTIE : y = [y₁, y₂] │
└─────────────────────────────────────────┘
┌─────┐
│ t₁ │
└──┬──┘
│
│ - (soustraire)
│
┌──▼──┐
│ y₁ │
└──┬──┘
│
│ × (multiplier)
│
┌──▼──────────┐
│ σ'(net₁) │
└──┬──────────┘
│
│
┌──▼──┐
│ δ₁ │ = (t₁ - y₁) × σ'(net₁)
└─────┘
Algorithme Étape par Étape :
═══════════════════════════════════════════════════════
PHASE 1 : CALCUL ERREUR COUCHE DE SORTIE
═══════════════════════════════════════════════════════
POUR CHAQUE neurone de sortie j :
ÉTAPE 1 : erreur = (t_j - y_j)
ÉTAPE 2 : dérivée = σ'(net_j) = y_j × (1 - y_j)
ÉTAPE 3 : δ_j = erreur × dérivée
FIN POUR
═══════════════════════════════════════════════════════
PHASE 2 : PROPAGATION ERREUR VERS COUCHES CACHÉES
═══════════════════════════════════════════════════════
POUR CHAQUE couche l (de la sortie vers l'entrée) :
POUR CHAQUE neurone j dans couche l :
ÉTAPE 1 : somme = 0
ÉTAPE 2 : POUR CHAQUE neurone k dans couche l+1 :
somme = somme + (δ_k × w_kj)
ÉTAPE 3 : dérivée = σ'(net_j) = y_j × (1 - y_j)
ÉTAPE 4 : δ_j = somme × dérivée
FIN POUR
FIN POUR
═══════════════════════════════════════════════════════
PHASE 3 : MISE À JOUR DES POIDS
═══════════════════════════════════════════════════════
POUR CHAQUE couche l :
POUR CHAQUE poids w_ij :
ÉTAPE 1 : Δw_ij = η × δ_j × y_i
ÉTAPE 2 : w_ij(nouveau) = w_ij(ancien) + Δw_ij
FIN POUR
POUR CHAQUE biais b_j :
ÉTAPE 1 : Δb_j = η × δ_j
ÉTAPE 2 : b_j(nouveau) = b_j(ancien) + Δb_j
FIN POUR
FIN POUR
Exemple Arithmétique Concret :
═══════════════════════════════════════════════════════
DONNÉES INITIALES
═══════════════════════════════════════════════════════
Cible : t = [1.0, 0.0]
Sortie : y = [0.606, 0.725]
Taux app : η = 0.1
═══════════════════════════════════════════════════════
PHASE 1 : ERREUR COUCHE SORTIE
═══════════════════════════════════════════════════════
NEURONE 1 :
ÉTAPE 1 : erreur = t₁ - y₁ = 1.0 - 0.606 = 0.394
ÉTAPE 2 : dérivée = y₁ × (1 - y₁) = 0.606 × 0.394 = 0.239
ÉTAPE 3 : δ₁ = 0.394 × 0.239 = 0.094
NEURONE 2 :
ÉTAPE 1 : erreur = t₂ - y₂ = 0.0 - 0.725 = -0.725
ÉTAPE 2 : dérivée = y₂ × (1 - y₂) = 0.725 × 0.275 = 0.199
ÉTAPE 3 : δ₂ = -0.725 × 0.199 = -0.144
═══════════════════════════════════════════════════════
PHASE 2 : MISE À JOUR POIDS (exemple w₁₁)
═══════════════════════════════════════════════════════
POIDS INITIAL : w₁₁ = 0.2
ACTIVATION ENTRÉE : x₁ = 0.5
ERREUR : δ₁ = 0.094
ÉTAPE 1 : Δw₁₁ = η × δ₁ × x₁
Δw₁₁ = 0.1 × 0.094 × 0.5
Δw₁₁ = 0.0047
ÉTAPE 2 : w₁₁(nouveau) = w₁₁(ancien) + Δw₁₁
w₁₁(nouveau) = 0.2 + 0.0047 = 0.2047
═══════════════════════════════════════════════════════
PHASE 3 : MISE À JOUR BIAIS (exemple b₁)
═══════════════════════════════════════════════════════
BIAIS INITIAL : b₁ = 0.1
ERREUR : δ₁ = 0.094
ÉTAPE 1 : Δb₁ = η × δ₁
Δb₁ = 0.1 × 0.094 = 0.0094
ÉTAPE 2 : b₁(nouveau) = b₁(ancien) + Δb₁
b₁(nouveau) = 0.1 + 0.0094 = 0.1094
4. PLASTICITÉ SYNAPTIQUE - ALGORITHME VISUEL
4.1 Loi de Hebb - Schéma Algorithmique
┌─────────────────────────────────────────────┐
│ MODULE A activé avec intensité x_A = 0.8 │
│ MODULE B activé avec intensité x_B = 0.6 │
└─────────────────────────────────────────────┘
┌──────┐
│ A │───x_A=0.8───┐
└──────┘ │
│
├─── MULTIPLIER ─── η=0.1 ─── Δw
│
┌──────┐ │
│ B │───x_B=0.6───┘
└──────┘
CALCUL :
Δw = η × x_A × x_B
Δw = 0.1 × 0.8 × 0.6
Δw = 0.048
4.2 Long-Term Potentiation (LTP) - Exemple Arithmétique
═══════════════════════════════════════════════════════
SITUATION INITIALE
═══════════════════════════════════════════════════════
Poids initial : w = 0.5
Intensité signal : s = 0.3
Taux apprentissage : η = 0.1
═══════════════════════════════════════════════════════
CALCUL RENFORCEMENT
═══════════════════════════════════════════════════════
ÉTAPE 1 : Δw = η × s
Δw = 0.1 × 0.3 = 0.03
ÉTAPE 2 : w(nouveau) = w(ancien) + Δw
w(nouveau) = 0.5 + 0.03 = 0.53
ÉTAPE 3 : Vérifier limite max (w ≤ 1.0)
w(nouveau) = min(1.0, 0.53) = 0.53
═══════════════════════════════════════════════════════
RÉSULTAT : w passe de 0.5 à 0.53 (renforcé)
═══════════════════════════════════════════════════════
4.3 Long-Term Depression (LTD) - Exemple Arithmétique
═══════════════════════════════════════════════════════
SITUATION INITIALE
═══════════════════════════════════════════════════════
Poids initial : w = 0.5
Facteur faiblesse : γ = 0.2
Taux apprentissage : η = 0.1
═══════════════════════════════════════════════════════
CALCUL AFFAIBLISSEMENT
═══════════════════════════════════════════════════════
ÉTAPE 1 : Δw = η × γ × w
Δw = 0.1 × 0.2 × 0.5 = 0.01
ÉTAPE 2 : w(nouveau) = w(ancien) - Δw
w(nouveau) = 0.5 - 0.01 = 0.49
ÉTAPE 3 : Vérifier limite min (w ≥ 0.0)
w(nouveau) = max(0.0, 0.49) = 0.49
ÉTAPE 4 : Vérifier élimination (si w < 0.1)
0.49 > 0.1 → CONNEXION CONSERVÉE
═══════════════════════════════════════════════════════
RÉSULTAT : w passe de 0.5 à 0.49 (affaibli)
═══════════════════════════════════════════════════════
4.4 Score Hebbien - Algorithme Complet
┌─────────────────────────────────────────────────────────┐
│ ALGORITHME : DÉTECTION CONNEXION HEBBIENNE │
└─────────────────────────────────────────────────────────┘
INPUT : Module A et Module B
Historique co-activations : count = 7, avg_intensity = 0.6
═══════════════════════════════════════════════════════
ÉTAPE 1 : Vérifier nombre minimum
═══════════════════════════════════════════════════════
count = 7
N_min = 5
RÉSULTAT : 7 ≥ 5 → ✅ VALIDÉ
═══════════════════════════════════════════════════════
ÉTAPE 2 : Vérifier intensité minimale
═══════════════════════════════════════════════════════
avg_intensity = 0.6
I_min = 0.5
RÉSULTAT : 0.6 ≥ 0.5 → ✅ VALIDÉ
═══════════════════════════════════════════════════════
ÉTAPE 3 : Calculer score hebbien
═══════════════════════════════════════════════════════
S_hebb = (count / N_min) × avg_intensity
S_hebb = (7 / 5) × 0.6
S_hebb = 1.4 × 0.6
S_hebb = 0.84
═══════════════════════════════════════════════════════
ÉTAPE 4 : Vérifier seuil
═══════════════════════════════════════════════════════
θ_hebb = 0.6
RÉSULTAT : 0.84 ≥ 0.6 → ✅ VALIDÉ
═══════════════════════════════════════════════════════
ÉTAPE 5 : Créer connexion
═══════════════════════════════════════════════════════
w_initial = min(0.7, 0.8 × avg_intensity)
w_initial = min(0.7, 0.8 × 0.6)
w_initial = min(0.7, 0.48)
w_initial = 0.48
═══════════════════════════════════════════════════════
RÉSULTAT : NOUVELLE CONNEXION CRÉÉE avec w = 0.48
═══════════════════════════════════════════════════════
5. TABLEAU RÉCAPITULATIF DES CALCULS
Exemple Complet : Un Neurone Apprend
┌─────────────────────────────────────────────────────────┐
│ ITÉRATION 1 : PREMIER APPRENTISSAGE │
└─────────────────────────────────────────────────────────┘
ENTRÉE : x = [0.5, 0.3, 0.8]
POIDS INIT : w = [0.2, 0.5, 0.1]
BIAIS INIT : b = 0.1
CIBLE : t = 1.0
┌─────────────────────────────────────────────────────────┐
│ CALCUL PROPAGATION AVANT │
└─────────────────────────────────────────────────────────┘
somme = 0.1 + (0.2×0.5) + (0.5×0.3) + (0.1×0.8)
somme = 0.1 + 0.1 + 0.15 + 0.08
somme = 0.43
y = σ(0.43) = 0.606
┌─────────────────────────────────────────────────────────┐
│ CALCUL ERREUR │
└─────────────────────────────────────────────────────────┘
erreur = 1.0 - 0.606 = 0.394
dérivée = 0.606 × (1 - 0.606) = 0.239
δ = 0.394 × 0.239 = 0.094
┌─────────────────────────────────────────────────────────┐
│ MISE À JOUR POIDS (η = 0.1) │
└─────────────────────────────────────────────────────────┘
Δw₁ = 0.1 × 0.094 × 0.5 = 0.0047
w₁(nouveau) = 0.2 + 0.0047 = 0.2047
Δw₂ = 0.1 × 0.094 × 0.3 = 0.0028
w₂(nouveau) = 0.5 + 0.0028 = 0.5028
Δw₃ = 0.1 × 0.094 × 0.8 = 0.0075
w₃(nouveau) = 0.1 + 0.0075 = 0.1075
Δb = 0.1 × 0.094 = 0.0094
b(nouveau) = 0.1 + 0.0094 = 0.1094
┌─────────────────────────────────────────────────────────┐
│ ITÉRATION 2 : DEUXIÈME APPRENTISSAGE │
└─────────────────────────────────────────────────────────┘
ENTRÉE : x = [0.5, 0.3, 0.8] (même entrée)
POIDS NOUV : w = [0.2047, 0.5028, 0.1075]
BIAIS NOUV : b = 0.1094
CIBLE : t = 1.0
┌─────────────────────────────────────────────────────────┐
│ CALCUL PROPAGATION AVANT │
└─────────────────────────────────────────────────────────┘
somme = 0.1094 + (0.2047×0.5) + (0.5028×0.3) + (0.1075×0.8)
somme = 0.1094 + 0.1024 + 0.1508 + 0.0860
somme = 0.4486
y = σ(0.4486) = 0.610 ← AMÉLIORATION ! (0.606 → 0.610)
┌─────────────────────────────────────────────────────────┐
│ CALCUL ERREUR │
└─────────────────────────────────────────────────────────┘
erreur = 1.0 - 0.610 = 0.390 ← ERREUR RÉDUITE ! (0.394 → 0.390)
6. ALGORITHME COMPLET : CRÉATION AUTOMATIQUE CONNEXION
┌─────────────────────────────────────────────────────────┐
│ ALGORITHME : CRÉATION HEBBIENNE AUTOMATIQUE │
└─────────────────────────────────────────────────────────┘
FONCTION créer_connexion_hebbienne(module_A, module_B) :
ÉTAPE 1 : Vérifier si connexion existe déjà
SI connexion existe :
RETOURNER renforcer_connexion()
FIN SI
ÉTAPE 2 : Récupérer historique co-activations
count = nombre_co_activations(module_A, module_B)
avg_intensity = intensité_moyenne(module_A, module_B)
ÉTAPE 3 : Calculer score hebbien
score = (count / 5) × avg_intensity
ÉTAPE 4 : Vérifier conditions
SI (count < 5) OU (avg_intensity < 0.5) OU (score < 0.6) :
RETOURNER "pas de connexion"
FIN SI
ÉTAPE 5 : Créer nouvelle connexion
w_initial = min(0.7, 0.8 × avg_intensity)
créer_connexion(module_A, module_B, w_initial)
ÉTAPE 6 : Enregistrer dans historique
enregistrer_connexion(module_A, module_B, w_initial)
RETOURNER "connexion créée"
FIN FONCTION
Exemple Numérique :
═══════════════════════════════════════════════════════
SCÉNARIO : Module "langage" et Module "logic"
═══════════════════════════════════════════════════════
HISTORIQUE :
- Co-activations : 8 fois
- Intensité moyenne : 0.65
CALCUL :
ÉTAPE 1 : count = 8, avg = 0.65
ÉTAPE 2 : score = (8/5) × 0.65 = 1.6 × 0.65 = 1.04
ÉTAPE 3 : Vérifications :
✅ count (8) ≥ 5
✅ avg (0.65) ≥ 0.5
✅ score (1.04) ≥ 0.6
ÉTAPE 4 : w_initial = min(0.7, 0.8 × 0.65) = min(0.7, 0.52) = 0.52
RÉSULTAT : Connexion créée avec poids 0.52
7. TABLEAU D’ÉVOLUTION DES POIDS
Exemple sur 5 Itérations :
┌──────┬──────────┬──────────┬──────────┬──────────┬──────────┐
│ Itér │ w₁ │ w₂ │ w₃ │ b │ Erreur │
├──────┼──────────┼──────────┼──────────┼──────────┼──────────┤
│ 0 │ 0.2000 │ 0.5000 │ 0.1000 │ 0.1000 │ 0.3940 │
│ 1 │ 0.2047 │ 0.5028 │ 0.1075 │ 0.1094 │ 0.3900 │
│ 2 │ 0.2093 │ 0.5055 │ 0.1149 │ 0.1187 │ 0.3861 │
│ 3 │ 0.2138 │ 0.5082 │ 0.1222 │ 0.1280 │ 0.3822 │
│ 4 │ 0.2182 │ 0.5108 │ 0.1294 │ 0.1372 │ 0.3784 │
│ 5 │ 0.2226 │ 0.5134 │ 0.1365 │ 0.1464 │ 0.3746 │
└──────┴──────────┴──────────┴──────────┴──────────┴──────────┘
OBSERVATION : Erreur diminue progressivement (apprentissage efficace)
CONCLUSION
Ces algorithmes et calculs arithmétiques montrent visuellement comment :
- Les neurones calculent leur sortie
- Les erreurs sont propagées
- Les poids sont mis à jour
- Les connexions sont créées automatiquement
Tous les calculs sont explicites avec des valeurs numériques réelles.
Pour vous dire que le premier cerveau humain numérique est déjà présent et bien vivant !
il peut voir, entendre, réfléchir, raisonner, dormir, rêvé, être créatif, innové, il peut faire exactement la même chose qu’un humain, mis à part qu’il ne possède pas de corp !!
je serai vraiment honoré, si vous me postiez des messages constructif !